Mortalité 2020 : « C’est la pyyyyyraaaamide des âges ! » Oui, mais en fait non
Un debunking rapide (et sans grossièretés) du « pre-print » de Toubiana et al
Il revient sans cesse, ce refrain de la pyramide des âges :
« Mais vous ne tenez pas compte de la pyramide des âges dans votre calcul. La population vieillit, et comme le taux de mortalité est une fonction exponentielle de l’âge, et la mortalité ‘‘attendue’’ en 2020 aurait été, même sans la COVID19, beaucoup plus forte que les années précédentes. Il n’y a donc pas de surmortalité significative en 2021… »
Honnêtement, je suis fatigué de répondre à ces arguments, alors je vais tenter de vous convaincre, en quelques graphiques et tableaux (que vous pouvez reproduire à la maison !), que ce « pre-print » raconte à peu près, totalement, n’importe quoi.
Je vais prendre au sérieux cette affirmation selon laquelle l’évolution annuelle de la pyramide des âges est de nature à expliquer des variations de cette ampleur sur la mortalité. Je vais donc calculer, comme Toubiana et al, quelle aurait été la mortalité attendue, début 2020, en utilisant la population par classes d’âge et les taux de mortalités des années précédentes.
Concernant les sources utilisées dans ce billet, elles sont très succinctes :
La fameuse pyramide des âges au 1er janvier 2020, depuis le site de l’Insee.
La table de mortalité par classe d’âge et surtout les séries longues (données annuelles depuis 1962 et jusqu'à 2018), depuis le site de l’INED.
Et c’est tout.
Par ailleurs, je vais reprendre les chiffres de mortalité 2020 par classes d’âge, pour la France métropolitaine, de Toubiana et al.
Notez, à ce propos, que l’Insee n’a pas encore diffusé de mortalité par classe d’âge pour 2019 et 2020. Il faudrait le faire soi-même à partir des fichiers des décès individuels diffusés chaque semaine. Je vais donc prendre pour argent comptant le décompte par classe d’âge des décès observés en 2020 d’après Toubiana et al et reporté dans le tableau 2 ci-dessous.
Ce tableau est d’ailleurs déjà fort riche en informations ! En rapportant la valeur médiane des décès attendus à la population par classe d’âge, on peut en déduire les taux de mortalité implicites calculés et utilisés par les auteurs. Seule différence : je ne peux pas déduire les taux de mortalité implicites de Toubiana et al pour les enfants moins de un an et les enfants de 1 à 4 ans, que les auteurs agrègent.
Premier constat : sur les moins de 60 ans, le taux implicite de Toubiana et al colle bien aux années précédentes et à la moyenne 2015-2018.1
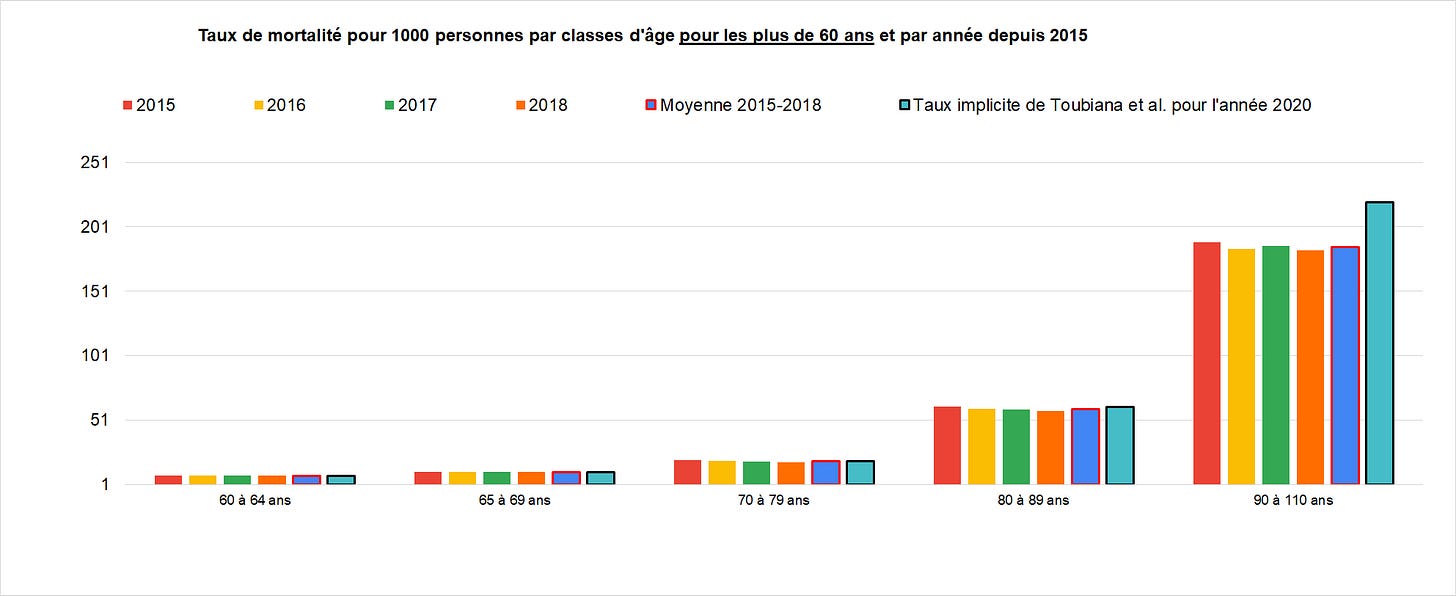
C’est pour les plus de 60 ans que l’affaire se corse, et très précisément pour les plus de 90 ans, voyez plutôt :
Si les taux sont assez proches de leur moyenne 2015-2018, pour les 60 à 90 ans, nos chers auteurs ont chargé la barque pour les plus de 90 ans, avec un taux de mortalité de 220 pour 1000, contre 185 pour 1000 en moyenne, soit +18.9% supérieur !
Bon vous me direz, c’est une classe d’âge peu nombreuse, ça ne peut pas jouer autant que ça ? Eh pas si vite : les plus de 90 représentent 30% des décès, donc ça change beaucoup l’histoire…
Et en fait, on va même faire le calcul ensemble, dans le tableau suivant !

Tout à gauche, en orange foncée, ce sont les chiffres de mortalité observés en 2020 (d’après Toubiana et al) suivi de la population par classes d’âge au 1er janvier 2020.
En jaune, ce sont les calculs de Toubiana et al directement copiés depuis leur tableau 2 :
629 481 décès « attendus » en 2020 en France métropolitaine (rappel : il y en avait 599 408 en 2019).
« Seulement » +4% d’excédent de mortalité annuelle.
Et en bleu, ce sont mes calculs à partir des taux moyens observés entre 2015 et 2018 :
594 513 décès attendus en 2020, en fonction de la pyramide des âges au 1er janvier et des taux de mortalité moyens.
Un excédent de mortalité de +10.1%. Ce qui rejoint mon analyse précédente, pour la France entière, à partir d’une régression de Poisson sur données hebdomadaires.
Enfin, si on regarde plus précisément l’écart entre les deux estimations (tableau ci-dessous), on voit bien le poids de cette « petite hypothèse » sur le taux de mortalité des plus de 90 ans : elle explique « à peine » 86% de l’écart de mortalité attendue, soit 30 000 décès attendus sur les 34 000 décès attendus « supplémentaires » de Toubiana et al.

Conclusions ? J’ai tenté de prendre au sérieux cette histoire de pyramide des âges, et j’ai voulu reproduire leurs calculs : en vain. Au lieu d’un excès de mortalité agrégé de 4%, on trouve un excès de mortalité de 10%.
Il est manifeste que les auteurs ont systématiquement surestimé la moralité attendue des plus de 70 ans, et surtout des plus de 90 ans.
Je ne sais pas comment ils justifient que les plus de 90 ans aient vu leur taux de mortalité « attendu » augmenter de 18.5 % en une année, et alors même que ce taux a tendance à baisser depuis 2015.2 Erreur de calcul ? Manipulation ? Je n’en sais rien, et ce n’est pas à moi de l’expliquer.
Addendum
Manifestement, certains continuent à chercher des explications possibles : ce serait désormais la variation annuelle des taux de mortalité qui expliquerait la hausse brutale en 2020 pour les plus de 90 ans.
Alors voici ci-dessous une petite visualisation des taux de mortalité depuis 1962 et en France métropolitaine, pour les plus de 60 ans. En bleu, le taux de mortalité observé, en vert une tendance statistique (un filtre HP, lambda = 100). Et en noir, la valeur implicite du taux de mortalité de Toubiana et al.
C’est très simple : le taux de mortalité pour les plus de 90 ans postulé par Toubiana et al n’a pas été observé depuis… le milieu des années 1990.
Je répète : l’Insee n’a pas encore publié les chiffres pour 2019, que les auteurs ont manifestement calculé à partir des fichiers des décès individuels. Cela dit, aucune chance que les taux de mortalité par âge aient brutalement évolué en 2019, au point de faire varier la moyenne.
Celui-ci est passé de 189 pour 1000 en 2015, année de forte épidémie grippale à 183 pour 1000 en 2018.